Kävin läpi kaikki 101 Matikkatuutorin kanssa käytyä keskustelua ja tarkistin oliko tekoäly onnistunut vai epäonnistunut ohjauksessaan. Epäonnistumiseksi laskettiin heti sellainen keskustelu, jossa tekoäly jossain vaiheessa hallusinoi. Onnistumiset ovat siis täydellisiä onnistumisia keskustelun jokaisessa vaiheessa. Tulos näyttää seuraavalle:
Onnistui: 86 kpl
Epäonnistui: 15 kpl
Onnistumisprosentiksi tulee näin ollen n. 85%. Jos laskuista jätetään pois ne osa-alueet, joilla tekoälyn on koettu toimivan epäluotettavasti, lähestytään jo 100% luotettavuutta. Esimerkiksi geometrian tehtävät olivat tekoälylle vaikeita.
Mikä on Matikkatuutori?
AIHackEd-hankkeen yhtenä tavoitteena on tutkia, miten tekoälyä voidaan hyödyntää oppimisen apuna. Eräs käyttötapa on hyödyntää generatiivista tekoälyä ohjeistamalla sitä toimimaan jonkun tietyn aihealueen tuutorina, joka antaa oppijalle vinkkejä siitä, miten hänen pitäisi lähteä etenemään oppijan esittämän ongelman ratkaisemiseksi.
GPT 3.5 mallin on todettu olevan matemaattisten ongelmien ratkaisemisen suhteen varsin epäluotettava. Tämä on tietenkin aika luonnollista, sillä suuret kielimallit eivät ole optimaalisia juuri matemaattisten ongelmien ratkaisemiseen. Yllättäen kuitenkin OpenAI:n tuoreempi GPT 4 on jo asian suhteen aivan eri luokkaa. GPT 3.5- ja 4-versioiden välistä ”kypsyyseroa” onkin verrattu joissain yhteyksissä lapsen ja aikuisen väliseen kehityseroon. GPT 3.5 on noin 6-vuotiaan tasolla, kun taas GPT 4 on ensimmäinen aikuisiän ylittävä kielimalli. AIHackEdissa kehitettävä Matikkatuutori on rakennettu GPT 4 APIa käyttäen.
Mitä tekoälyn valmentaminen tarkoittaa?
Matikkatuutori on yksi esimerkki tekoälybotista, jota on valmennettu toimimaan tietyllä tavalla. Valmentamista voi kuka tahansa kokeilla vaikkapa ChatGPT:n ilmaisversiolla antamalla ensimmäisessä promptissa tekoälylle toimintaohjeet jatkokeskustelua ajatellen. Matikkatuutorin ensimmäisessä kokeiluversiossa ohjeena esimerkiksi oli ” Olet avulias matematiikkabotti, joka auttaa tehtävässä antaen seuraavan välivaiheen, mutta ei saa kertoa suoraa vastausta tähän tehtävään:” + kysymys + ”Kirjoita matemaattinen teksti latex muodossa ja \( ja \) ympäröiminä.” Matikkatuutoria käyttäessä opiskelija ei näe valmennustekstiä, vaan se on ”rakennettu sisään” botin toimintaan.
Koska generatiivisten tekoälyjen toiminnasta tiedetään vielä varsin vähän, valikoitui hankkeessa luonnolliseksi kehittämisstrategiaksi mahdollisimman varhaisen kehitysvaiheen testaaminen opiskelijoilla, jotta saadaan heti dataa siitä, että toimiiko botti halutulla tavalla ja toisaalta siitä, miten hyvin opiskelijat osaavat keskustelua tekoälyn kanssa mistäkin aiheista viedä eteenpäin.
Millainen Matikkatuutorin esiversio on?

Matikkatuutorin ensimmäisessä versiossa opiskelijaa pyydetään ensin kirjoittamaan ja ”lukitsemaan” tehtävä, josta hän haluaa käydä tekoälyn kanssa keskustelua. Tämän jälkeen häntä kehotetaan käymään tekoälyn kanssa keskustelua samalla tavalla kuin keskustelua käytäisiin luokassa opettajan kanssa.
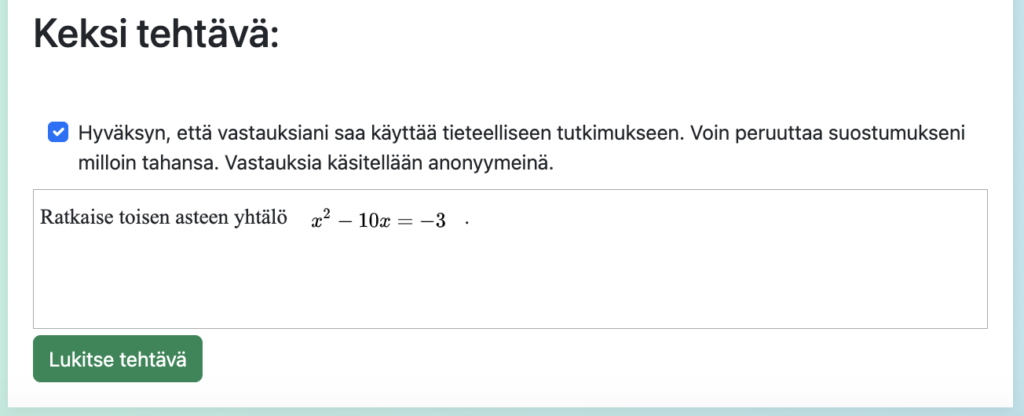
Matemaattisen notaation syöttämisen helpottamiseksi keskustelukenttään on upotettu Abitista tuttu matikkaeditori. Halutessaan opiskelijalla oli mahdollisuus myös ruksittaa hyväksyntä sille, että keskusteluja voidaan käyttää anonyymisti tieteellisessä tutkimuksessa.

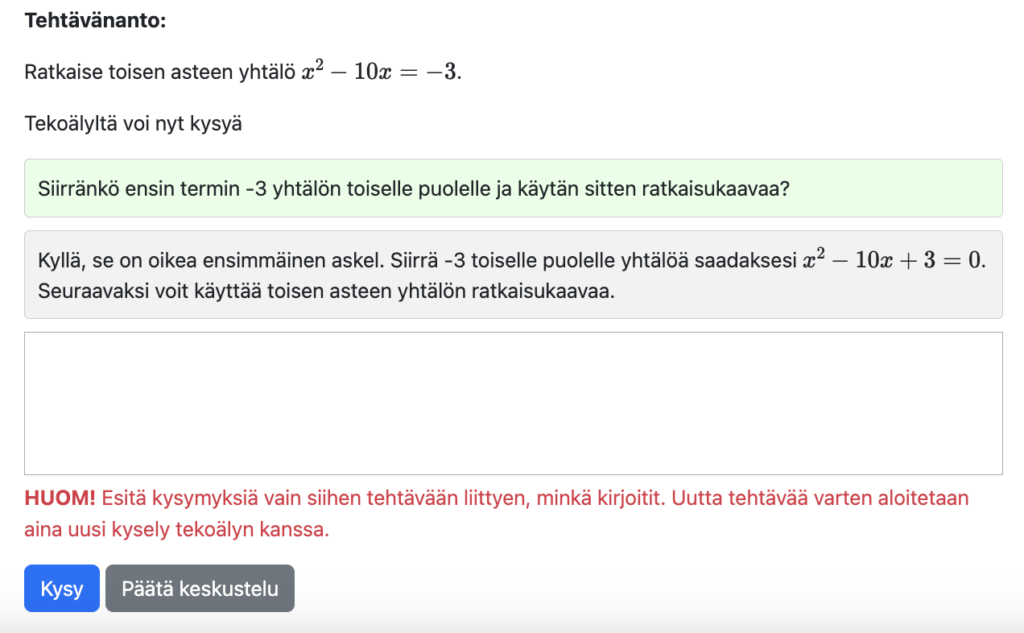
Lopuksi opiskelijaa kehotetaan aloittamaan aina uudesta aiheesta uusi keskustelu, sekä vastaamaan lyhyeen palautekyselyyn.
Dataa ja analyysiä
Opettajan ja tutkijan kannalta mielenkiintoista on data jota keskusteluista saadaan. Tässä niistä (tutkimusluvan antaneista) muutamia otteita.
Alussa näkyy suuremmalla fontilla opiskelijan lukitsema tehtävä, jonka jälkeen keskustelu on pienemmällä fontilla. Punaiset ovat opiskelijan kirjoittamia ja mustat tekoälyn. Jokaisen kuvankaappauksen alapuolella on lyhyt pohdinta ja analyysi.


Monesti opiskelija aloitti keskustelun pyytämällä apua, tervehtimällä tai kysymällä suoraan miten tehtävässä pitäisi lähteä liikkeelle. Myös suoraa vastausta pyydettiin usein, mutta tekoäly oli koulutettu olemaan antamatta sitä suoraan, vaan neuvomaan askel askeleelta eteenpäin ratkaisupolulla. Tämä ei tarkoita sitä etteikö tekoälyä saa vastausta antamaan suostuttelemalla, joka suurilla kielimalleilla on yksi ongelmallinen piirre.

Yksinkertaisesta sanallisesta todennäköisyystehtävästä tekoäly suoriutui varsin hyvin. Toisin Sanalliset tehtävät muutoinkin eivät näytä suurille kielimalleille olevan suuri ongelma verrattuna matemaattisella notaatiolla kirjoitettuihin tehtäviin.

Tässä opiskelija onnistui ohjaamaan tekoälyä neuvomaan tehtävän ratkaisemisessa hänen haluamallaan tavalla.

Tässä yhtälöparin ratkaisutehtävässä tekoäly ohjasi opiskelijaa käyttämään sijoituskeinoa.

Kaksiosaisessa asuntolainaa käsittelevässä tehtävässä tekoäly käytti annuiteetin laskemiseen kaavaa, joka on eri muodossa kuin MAOL-taulukoista löytyvä vastaava. Se teki myös laskuvirheen määrittäessään korkokerrointa r. Suurin virhe sille kuitenkin tuli maksuerien lukumäärien laskemisessa. Se ei nimittäin osannut poimia 20 vuoden laina-aikaa, vaan oletti virheellisesti sen olevan 48 kuukautta, vaikka kyseinen aikamääre liittyikin vuosikoron vaihtumisajankohtaan.

Toisessa asuntolainatehtävässä tekoäly ”syyllistyi” suostuttelulla vaihtamaan aluksi oikein laskemaansa arvoa. Suostuttelu on ollut yleinen ongelma varsinkin GPT:n versioissa 3 ja 3.5, joissa ChatGPT saatiin melko helposti suostuttelemalla väittämään älyttömyyksiä kuten ”4 = 5” tosiksi asioiksi. Tässä tehtävässä opiskelija sai vahingossa tekoälyä vaihtamaan mielipidettään korkokertoimen r suuruudesta.

Tästä trigonometristen funktioiden sovellustehtävästä tekoäly suoriutui mallikkaasti antaen oikean funktion tulokseksi.


Tässä tehtävässä opiskelija on palastellut tehtäväänsä tekoälylle valmiiksi. Tämä voi olla hyvä strategia sen sijaan, että kaikki tehtävän alakohdat kirjoitetaan heti aluksi tiedoksi. Sen jälkeen opiskelija on edennyt keskustelemalla eteenpäin, jolloin tekoälyn kannalta syntyy loogisempi jatkumo. Lopputulos on hyvä!

Tässä geometrisessa tehtävässä tekoäly on aluksi neuvonut piirtämisessä oikein. Seuraavassa vaiheessa opiskelija on kesken keskustelun vaihtanut kolmioiden pinta-alojen A, B, C ja D paikkoja, mikä voi olla huono strategia. Kolmion A pinta-alalle tekoäly ei onnistunut muodostamaan oikeaa lauseketta. Voi olla, että geometriset tehtävät ovat tekoälylle erityisen hankalia.
Mitä voitaisiin tehdä luotettavuuden parantamiseksi tiettyjen osa-alueiden välttämisen lisäksi?
Yksi keino voisi olla tekoälyn suostutteluongelman välttäminen. Käytännössä se voisi tarkoittaa sitä, että tekoäly ohjeistetaan olemaan ottamatta kantaa opiskelijan välivaiheen oikeellisuudesta. Toisaalta opiskelijaa voitaisiin valistaa suostuttelun problematiikasta, jolloin sitä tapahtuu vähemmän ja opiskelija osaa varautua siihen.
Toinen keino on keskustelustrategian kehittäminen. Aineistossa havaittiin keskusteluja, joissa opiskelija ei ollut laittanut ison tehtävän tapauksessa koko tehtävää ratkaistavaksi, vaan aloitti jostain tehtävän pienestä osasta rakentaen loogisen ratkaisupolun tekoälyn kanssa käytävän keskustelun avulla. Tämänkaltaisilla keinoilla voitaisiin blokata tekoälyn väärinkäsitykset pitkissä tehtävänannoissa, joissa yksittäisen sanan merkitys ratkaisun kannalta voi olla suuri. Ehkä tekoälyltä voisi myös aluksi kysyä, että miten tehtävänannon ymmärtää, jotta väärinymmärryksiltä vältyttäisiin?
Kolmas keino on pohtia sitä, mikä tekoälyn ja oppijan rooli keskusteluissa tulisi olla. Microsoft nimesi oman tekoälynsä copilotiksi. Nimi on kuvaava, sillä siihen sisältyy ajatus tekoälyn avustavasta roolista, kun varsinainen pilotti on itse sen käyttäjä. Matikkatuutorin ensimmäisessä versiossa opiskelijoiden keskustelun avaukset kuitenkin heittivät pallon heti aluksi tekoälylle. Ajatuksena voisi olla se, että opiskelija tuottaisikin ensin itse jotain ja tekoäly toimii rinnalla valmentajana ja ideoijana, copilottina.
Neljäs keino on rajata voimakkaasti osa-aluetta, jolla sparrattu tekoäly toimii. Tällöin tekoälylle annettava ohjeistus voi olla yksityiskohtaisempi ja toiminta on todennäköisemmin sellaista mitä halutaan. Rajaus voisi rajoittua esimerkiksi tietylle matematiikan osa-alueelle tai jopa yksittäiseen tehtävään.
Yhteenveto ja jatkokehitys
Lukion opiskelijoiden ymmärrys siitä, miten tekoäly toimii, on vielä varsin vajavaista. Se heijastuu suoraan taitoihin, joilla keskustelua tekoälyn kanssa viedään eteenpäin. Tähän opiskelijat tarvitsevat pikaisesti lisäoppia. Esimerkiksi useiden eri tehtävien ratkaiseminen samassa keskustelussa ei tuota hyvää lopputulosta keskustelulle.
Ensimmäiset havainnot datan pohjalta viittaavat myös siihen, että niillä opiskelijoilla, joilla matemaattisten ongelmien sanallistamisessa on ongelmia, oli
hankaluuksia myös käydä tekoälyn kanssa keskustelua. Tehtävän lukitseminen alussa ja keskustelun aloittaminen sanoilla ”Apua!” tai ”Miten pääsen alkuun?” passivoi opiskelijan ja heittää pallon heti tekoälylle.

Uudessa versiossa, nimeltään Matikkasparraaja, on edellä mainittuja ongelmia taklattu mm. poistamalla tehtävän lukitseminen keskustelun alussa ja tekemällä keskustelun aloittamisesta vapaamuotoisempaa. Lisäksi tekoälyä on ohjeistettu jatkamaan keskustelua esittämällä aina jokin sopiva jatkokysymys. Matikkasparraaja myös varmistaa opiskelijalta, onko sparraajan käyttämä menetelmä hänelle ennestään tuttu.
Matikkasparraaja on ollut käytössä vapaaehtoisena lisäapuna pitkän matematiikan kertauskursseilla muutamalla ryhmällä. Pian kerron raporttia, miten työväline on tarkoituksessaan toiminut!


